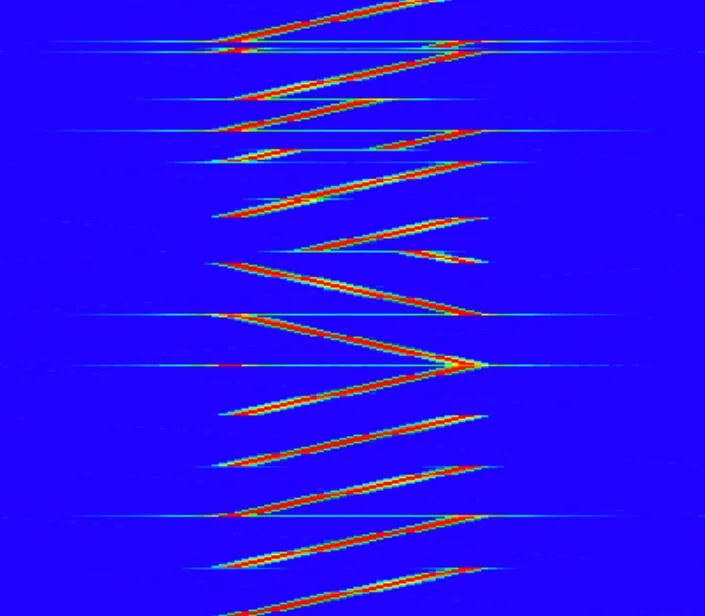
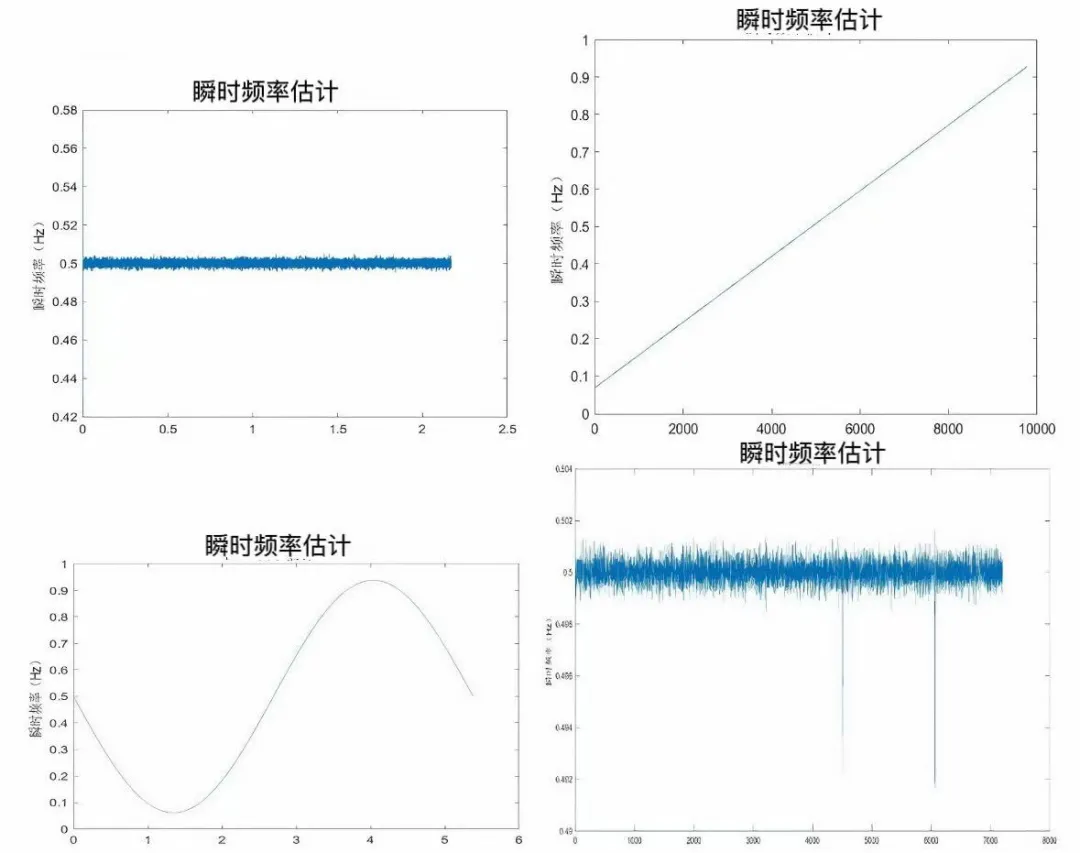
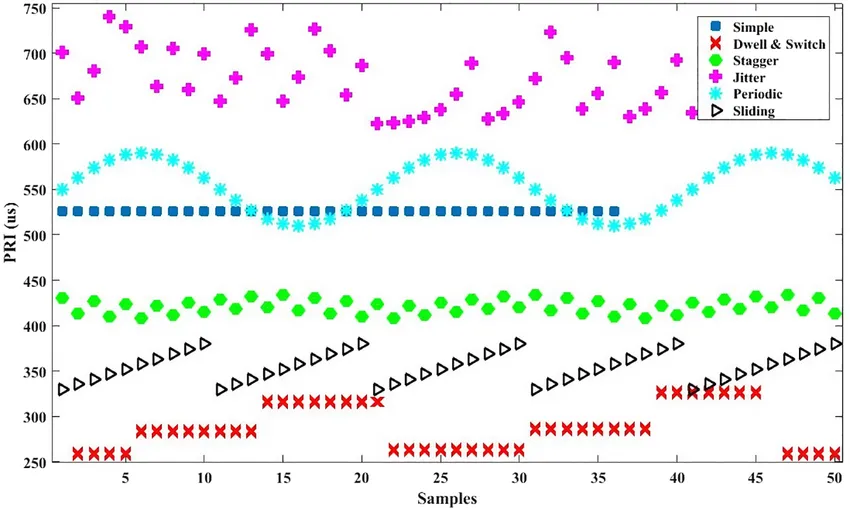
基于上述分析,我们可将各类脉冲的瞬时频率曲线作为输入,通过简单的神经网络实现分类。下面从网络原理、结构设计与验证实现三方面展开说明。
1.神经网络的核心原理
神经网络并非复杂神秘的技术,其基本单元是 “神经元”,网络本质是神经元的不同连接与组合。
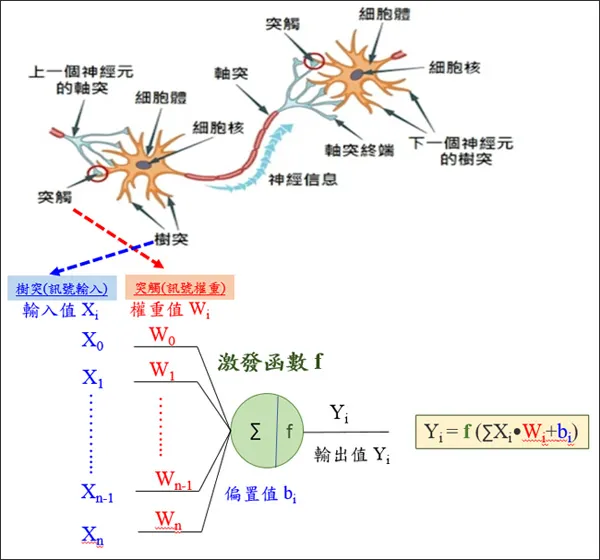
人工神经元的组成清晰:对输入信号进行线性加权求和、叠加偏置项后,再通过非线性激活函数处理,最终输出结果。具体结构可参考生物神经元与人工神经元的对比,如图4所示:
图4 生物神经元与人工神经元对比
正是这样简单的神经元,支撑起了AI技术的快速发展 —— 甚至直接推动英伟达成为市值五万亿美元的全球顶尖企业。相较于传统机器学习方法,神经网络的核心优势(微观层面)并非前端的线性加权,而是后端的非线性处理:这一环节使神经网络能以任意精度逼近紧致集上的连续函数,具备强大的拟合与分类能力。
2.轻量化网络结构设计
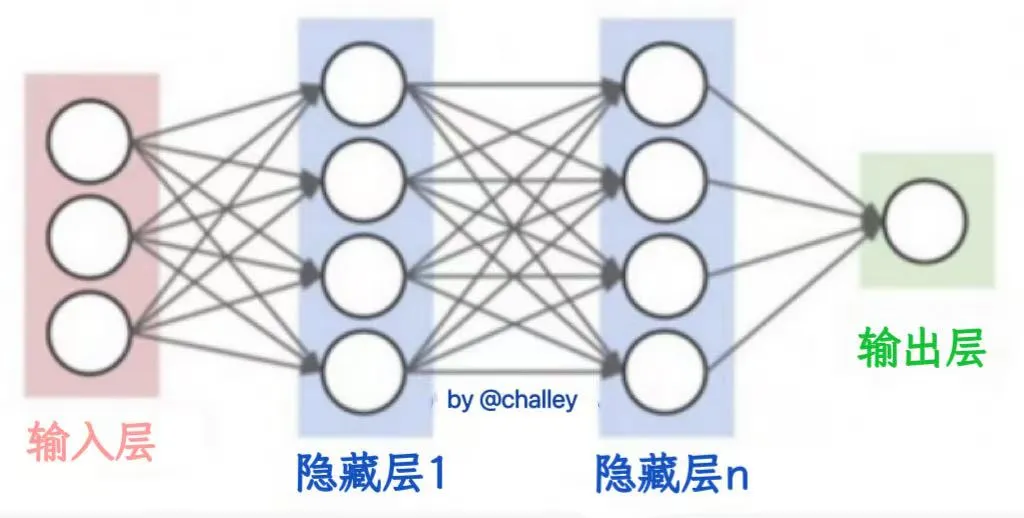
单个人工神经元可通过串联、并联组成隐藏层,多个隐藏层与输入层、输出层结合,便构成了用于分类的前馈神经网络,结构如下:
✔ 输入层:对应一维瞬时频率曲线(输入维度为“样本数×频率曲线采样点数”);
✔ 隐藏层:设置若干个隐藏层,下面示例三层,其神经元数量分别为256、128、32(通过轻量化设计降低计算量);
✔ 输出层:对应4种调制类型(输出维度为“样本数×4”,采用softmax激活函数输出分类概率)。
如图5所示,即可完成上述调制类型分类任务。
图5 多层神经网络示意图
3.基于MATLAB的验证实现
为简化环境搭建流程,省却搭建验证深度学习依赖库和环境的繁琐操作,可基于MATLAB快速验证模型效果。
首先配置net的各个训练参数,然后调用train函数进行训练,最后调用sim函数针对测试集数据SAMPLES_TEST进行验证。
关键代码如下:
% SAMPLES_TRAIN:训练样本矩阵(维度:N×M,N为训练样本数,M为瞬时频率曲线采样点数)
% LABELS:训练标签(维度:N×4,采用one-hot编码,4列分别对应CW、LFM、NLFM、相位编码)
% 1. 创建3隐藏层前馈神经网络(神经元数:256、128、32)
net = feedforwardnet([25612832], 'traingd');
% 2. 设置各层激活函数
net.layers{1}.transferFcn = 'logsig'; % 第1隐藏层:S型对数激活函数
net.layers{2}.transferFcn = 'logsig'; % 第2隐藏层:S型对数激活函数
net.layers{3}.transferFcn = 'logsig'; % 第3隐藏层:S型对数激活函数
net.layers{4}.transferFcn = 'softmax'; % 输出层:softmax函数(输出分类概率)
% 3. 配置训练参数
net.trainParam.lr = 0.01; % 学习率:0.01
net.trainParam.epochs = 200; % 训练轮数:200
net.trainParam.max_fail = 10; % 最大验证失败次数:10(默认6,提升容错性)
net.trainParam.goal = 1e-5; % 训练目标误差:1e-5
% 4. 模型训练与测试
[net, tr] = train(net, SAMPLES_TRAIN, LABELS); % 训练模型
val = sim(net, SAMPLES_TEST); % 测试集验证,(SAMPLES_TEST格式同训练集)
☞上述代码框可左右滑动噢!
该网络的权重参数与计算量,远小于近年常用的深度卷积神经网络(如GoogleNet、VGG)与循环神经网络(如LSTM)。若需进一步提升性能,也可替换为简单循环神经网络 —— 因输入为一维曲线数据,计算量仍可控。
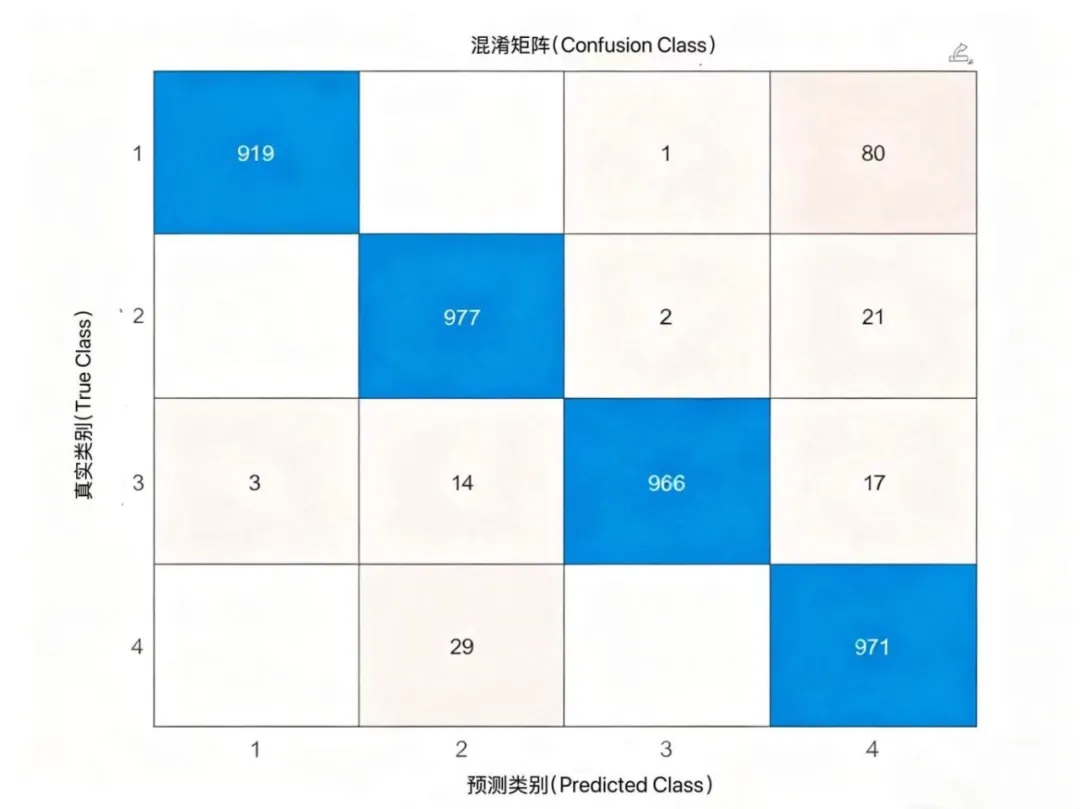
图6为四种脉内调制类型的分类测试结果(混淆矩阵),可见简单轻量化网络即可高效区分不同趋势曲线:
图6 四种调制类型的分类测试结果
从该案例可看出:神经网络类型虽多、规模虽在不断扩大,但实际应用中并非需追求“新颖”或“庞大”,当任务复杂度较低时,轻量化网络足以满足需求 —— 这在工程实践中意义重大,可直接降低软硬件资源消耗与功耗,尤其适配功耗敏感场景。